Fáry's theorem
In mathematics, Fáry's theorem states that any simple planar graph can be drawn without crossings so that its edges are straight line segments. That is, the ability to draw graph edges as curves instead of as straight line segments does not allow a larger class of graphs to be drawn. The theorem is named after István Fáry, although it was proved independently by Klaus Wagner (1936), Fáry (1948), and S. K. Stein (1951).
Contents |
Proof
Let 
be a simple planar graph with 
vertices; we may add edges if necessary so that is maximal planar. All faces of will be triangles, as we could add an edge into any face with more sides while preserving planarity, contradicting the assumption of maximal planarity. Choose some three vertices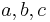 
forming a triangular face of 
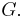We prove by induction on that there exists a straight-line embedding of in which triangle 
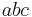is the outer face of the embedding. As a base case, the result is trivial when 
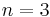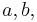and 
and 
are the only vertices in Otherwise, all vertices in have at least three neighbors.
By Euler's formula for planar graphs, has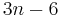 
edges; equivalently, if one defines the deficiency of a vertex 
in to be six minus the degree of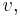 
the sum of the deficiencies is twelve. Each vertex in can have deficiency at most three, so there are at least four vertices with positive deficiency. In particular we can choose a vertex with at most five neighbors that is different from 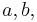and 
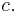Let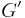 
be formed by removing from and retriangulating the face formed by removing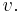 
By induction, 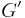has a straight line embedding in which abc is the outer face. Remove the added edges in 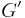, forming a polygon 
with at most five sides into which should be placed to complete the drawing. By the Art gallery theorem, there exists a point interior to at which can be placed so that the edges from to the vertices of do not cross any other edges, completing the proof.
The induction step of this proof is illustrated at right.
Related results
De Fraysseix, Pach and Pollack showed how to find in linear time a straight-line drawing in a grid with dimensions linear in the size of the graph. A similar method has been followed by Schnyder to prove enhanced bounds and a characterization of planarity based on the incidence partial order. His work stressed the existence of a particular partition of the edges of a maximal planar graph into three trees known as a Schnyder wood.
Tutte's spring theorem states that every 3-connected planar graph can be drawn on a plane without crossings so that its edges are straight line segments and an outside face is a convex polygon (Tutte 1963). It is so called because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
Steinitz's theorem states that every 3-connected planar graph can be represented as the edges of a convex polyhedron in three-dimensional space. A straight-line embedding of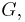 
of the type described by Tutte's theorem, may be formed by projecting such a polyhedral representation onto the plane.
The Circle packing theorem states that every planar graph may be represented as the intersection graph of a collection of non-crossing circles in the plane. Placing each vertex of the graph at the center of the corresponding circle leads to a straight line representation.
| Does every planar graph have a straight line representation in which all edge lengths are integers? |
Heiko Harborth raised the question of whether every planar graph has a straight line representation in which all edge lengths are integers.[1] The answer remains unknown as of 2009[update]. However, integer-distance straight line embeddings are known to exist for cubic graphs.[2]
Sachs (1983) raised the question of whether every graph with a linkless embedding in three-dimensional Euclidean space has a linkless embedding in which all edges are represented by straight line segments, analogously to Fáry's theorem for two-dimensional embeddings.
Notes
References
- Fáry, István (1948), "On straight-line representation of planar graphs", Acta Sci. Math. (Szeged) 11: 229–233, MR0026311.
- de Fraysseix, Hubert; Pach, János; Pollack, Richard (1988), "Small sets supporting Fary embeddings of planar graphs", Twentieth Annual ACM Symposium on Theory of Computing, pp. 426–433, doi:10.1145/62212.62254, ISBN 0897912640.
- de Fraysseix, Hubert; Pach, János; Pollack, Richard (1990), "How to draw a planar graph on a grid", Combinatorica 10: 41–51, doi:10.1007/BF02122694, MR1075065.
- Geelen, Jim; Guo, Anjie; McKinnon, David (2008), "Straight line embeddings of cubic planar graphs with integer edge lengths", J. Graph Theory 58 (3): 270–274, doi:10.1002/jgt.20304, http://www.math.uwaterloo.ca/~dmckinnon/Papers/Planar.pdf.
- Harborth, H.; Kemnitz, A.; Moller, M.; Sussenbach, A. (1987), "Ganzzahlige planare Darstellungen der platonischen Korper", Elem. Math. 42: 118–122.
- Kemnitz, A.; Harborth, H. (2001), "Plane integral drawings of planar graphs", Discrete Math. 236: 191–195, doi:10.1016/S0012-365X(00)00442-8.
- Mohar, Bojan (2003), Problems from the book Graphs on Surfaces, http://www.fmf.uni-lj.si/~mohar/Book/BookProblems.html.
- Mohar, Bojan; Thomassen, Carsten (2001), Graphs on Surfaces, Johns Hopkins University Press, pp. roblem 2.8.15, ISBN 0801866898.
- Sachs, Horst (1983), "On a spatial analogue of Kuratowski's theorem on planar graphs — An open problem", in Horowiecki, M.; Kennedy, J. W.; Sysło, M. M., Graph Theory: Proceedings of a Conference held in Łagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, 1018, Springer-Verlag, pp. 230–241, doi:10.1007/BFb0071633, ISBN 978-3-540-12687-4.
- Schnyder, Walter (1990), "Embedding planar graphs on the grid", Proc. 1st ACM/SIAM Symposium on Discrete Algorithms (SODA), pp. 138–148, http://portal.acm.org/citation.cfm?id=320176.320191.
- Stein, S. K. (1951), "Convex maps", Proceedings of the American Mathematical Society 2 (3): 464–466, doi:10.2307/2031777, JSTOR 2031777, MR0041425.
- Tutte, W. T. (1963), "How to draw a graph", Proceedings of the London Mathematical Society 13: 743–767, doi:10.1112/plms/s3-13.1.743, MR0158387.
- Wagner, Klaus (1936), "Bemerkungen zum Vierfarbenproblem", Jahresbericht. German. Math.-Verein. 46: 26–32, http://www.digizeitschriften.de/index.php?id=resolveppn&PPN=GDZPPN002131633.